Extending the Tusi Couple into Three Dimensions

For centuries, one elegant geometric construction has quietly demonstrated something profound: rotation can produce order.

The original Tusi Couple, developed by Nasir al-Din al-Tusi in the 13th century, showed how two circles in motion could generate a perfectly straight line. Not through randomness. Not through chance. But through pure geometric constraint.

That idea still matters.

But it does not have to stop at a line.

The Classical Foundation: Linear Motion from Rotation

The traditional Tusi Couple consists of:

One large circle
One smaller circle exactly half its radius
The smaller circle rolling inside the larger

When configured correctly, a point on the inner circle moves back and forth along a single straight axis. Despite originating from circular motion, the visible result is linear oscillation.

This is important because it demonstrates a principle:
Complex-looking motion can arise from simple geometric rules.

There is no randomness in the system. Every position is determined by the geometry alone.

But in its classical form, the motion is confined to a single plane.

Moving Beyond the Line: Hypotrochoids in Two Dimensions

If you adjust the strict radius relationship or change the tracing point’s offset, the straight line unfolds into looping curves known as hypotrochoids.

These curves:

Exist across both the X and Y axes
Form bounded, repeating structures
Remain deterministic
Never rely on entropy

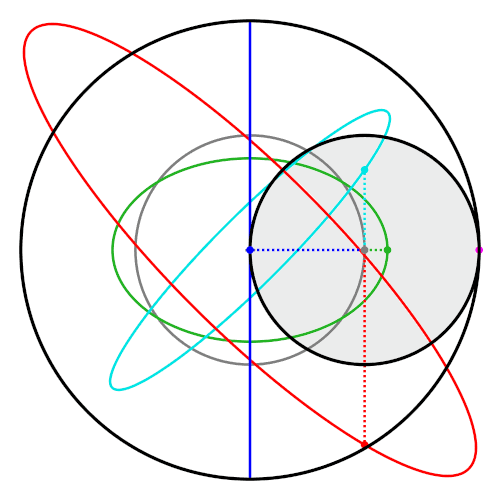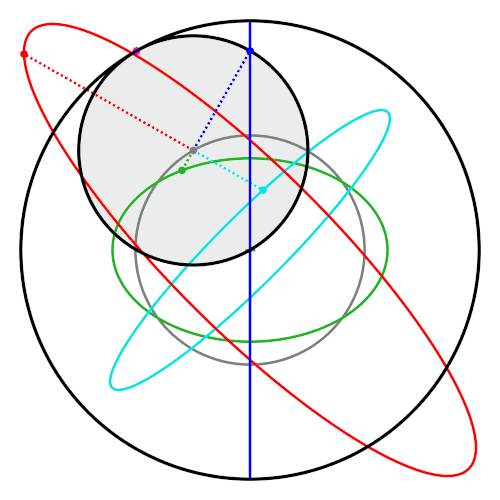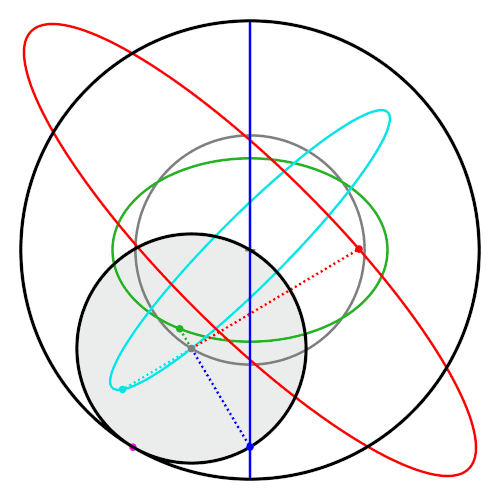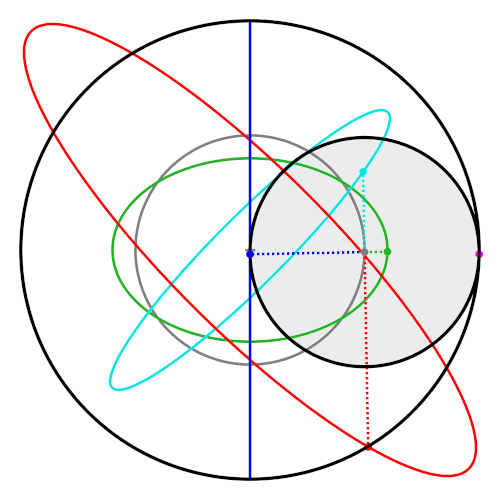
The system is still governed by geometry. The difference is freedom. Instead of collapsing rotation into a straight line, the motion now spreads across a plane.

The output becomes more intricate — but the underlying rule remains the same: motion is constrained, not random.

Still, it is flat.

The Limitation of Planar Geometry

The classical Tusi Couple exists in 1 dimension along the y axis. Its hypotrochoid variations exist in two dimensions along the x and y axes. All motion occurs on a flat surface. Even the most complex patterns never leave that plane.

That limitation is structural.

So the question becomes:

What happens if the geometry itself is no longer confined to 2D?

The Extension: The Tusi Volumetric Couple

The extension replaces circles with spheres.

Instead of:

A circle rolling inside a circle

We now have:

A sphere rotating within a larger spherical boundary

And instead of rotation confined to a single plane, motion is allowed independently across the X, Y, and Z axes.

This creates a Tusi Volumetric Couple — a three-dimensional generalisation of the original construction.

A tracing point attached to the inner sphere no longer generates a flat curve. It produces a spatial trajectory — a volumetric path evolving through three-dimensional space.

Hypotrochoid-style motion no longer lives on a sheet.
It exists in volume.

What This Actually Changes

This extension does not introduce randomness.
It does not introduce memory.
It does not introduce artificial intelligence.

What it introduces is dimensional freedom.

By allowing motion to unfold across X, Y, and Z simultaneously:

Paths can intersect spatially without overlapping
Motion can fold through depth rather than looping flat
Geometric relationships can evolve in ways impossible in 2D

The complexity increases because the available space increases.

The rules remain deterministic.

Why This Matters in Paranormal Systems

Many paranormal tools rely on noise-based systems — shuffled lists, radio fragments, entropy-driven selection.

Geometric systems operate differently.

In a Tusi-based framework:

Every output is a direct consequence of rotational relationships
No external randomness is required
No arbitrary resets are needed

The behaviour that emerges comes from structure alone.

Extending that structure into three dimensions expands the range of possible motion without abandoning determinism. Instead of producing flat oscillations or planar loops, the system produces volumetric trajectories that evolve continuously within spatial bounds.

The geometry does not guess.
It unfolds.

From Ancient Mathematics to Modern Application

The brilliance of the original Tusi Couple was showing that circular motion could generate a straight line. That was a revelation in its time.

The next step is recognising that the principle does not belong only to flat space.

By replacing circles with spheres and allowing full three-axis rotation, the construction becomes volumetric. Hypotrochoids are no longer confined to the page. They move through space.

The mathematics remains rooted in geometry.
The expansion is dimensional, not conceptual.

Sometimes progress is not about adding randomness.

Sometimes it is simply about allowing structure more room to move.

The Rebuttal

Claims that this system is “random”, “just noise”, or “no different from existing generators” demonstrate a fundamental misunderstanding of both the mathematics involved and the nature of deterministic systems.

The Tusi Volumetric Couple does not rely on entropy, shuffled datasets, radio input, or probabilistic selection. It is driven entirely by continuous geometric relationships. Every output is a direct consequence of persistent three-dimensional motion governed by fixed constraints. Nothing is chosen. Nothing is injected. Nothing is reset.

Random systems forget.
This system cannot.

Its current state is inseparable from its past, because the geometry itself is the memory. Each position exists only because of everything that preceded it. That alone places it outside the category of randomness, regardless of how unfamiliar or complex the output may appear.

Criticism that focuses on surface similarity — such as looping paths, fluctuating outputs, or non-repeating behaviour — mistakes appearance for mechanism. Two systems can look alike while functioning entirely differently. Imitating the shape of motion is trivial. Reproducing the underlying coherence is not.

This framework is not presented as a theoretical curve, a visual effect, or a novelty animation. It is a deterministic motion engine, designed to encode state, progression, and dependency through geometry rather than chance. Dismissing it as “just maths” is not a refutation — it is an admission that the critique has not progressed beyond the first layer.

If a system’s behaviour cannot be reproduced without breaking continuity, injecting noise, or resetting state, then it is not random — it is simply being misunderstood.

Origin of the Volumetric Extension

The three-dimensional extension of the Tusi principle presented here — referred to as the Tusi Volumetric Couple — was developed through my own independent research into geometric motion systems for structured output generation.

While the classical Tusi Couple and planar hypotrochoids are well established in mathematical literature, no documented framework was found that replaces the circular construction with rotating spheres to produce volumetric hypotrochoid-style trajectories across X, Y, and Z space.

The transition from planar circles to rotational spheres was not derived from an existing model, but emerged from experimentation with dimensional expansion of deterministic systems. The resulting construction preserves the geometric constraints of the original Tusi principle while allowing motion to evolve fully within three-dimensional space.

This volumetric formulation is therefore not a rediscovery of a named mathematical object, but an original extension built upon classical foundations.